Prologue Link to heading
Video games have this incredible ability to evoque certain feelings and states of mind on the people that play them. You can experience pretty much every emotion, starting from happiness, amazement, and wonder going all the way to sadness, frustation, and heartbreak. Games can make you laugh and cry, they can make you focus, and sometimes they make you think.
Factorio is a game that makes you think. It gives such fascinating production and logistics challenges to its players that sometimes they stop playing and write research papers about the problems they face in this game1. In the recently released Factorio Space Age expansion, a new feature was added that allows the player to gamble their way into having better versions of every item in the game: Quality.

(image source: fff-375)
Getting a complete understanding of the probabilities behind the mass production of quality items is not easy, and neither is converting this set of probabilities into workable flow rates. With this is mind, and after struggling with this myself, I have decided to write a series of blog posts detailing step by step the math required to truly understand quality. I will assume that the reader has played Factorio: Space Age and has a working understanding of the quality mechanic, but even if you haven’t played Factorio before, feel free to follow along. Without further ado, let’s begin:
Building the quality matrix Link to heading
When you insert a quality module in a assembler2, a new stat appears on the machine’s tooltip: Quality. The goal of this chapter is to convert this singular value into a probability matrix.
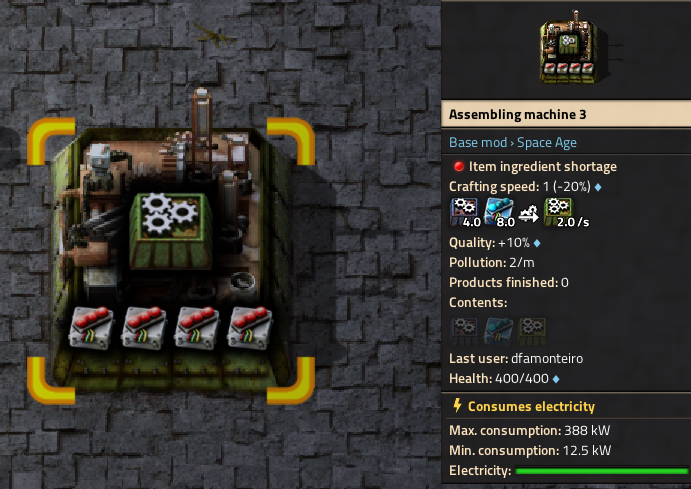
Each module contributes 2.5% quality chance for a grand total of 10%.
This quality chance, which I will call $q$ from now on, represents the probability of a machine crafting items of a higher quality than their ingredients. Please note that a quality upgrade of multiple tiers is entirely possible, but becomes more unlikely by a factor of 10 for every “bonus” quality upgrade. Using this knowledge we can craft a template quality upgrade probability table, which indicates the probability of ingredients of quality Input turning into items of quality Output:
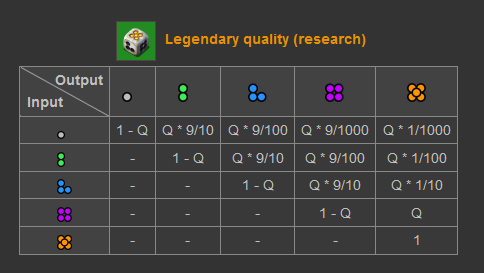
(image source: Factorio Wiki)
At this point, we have a solid enough understanding of quality for us to try to replicate some of the results found in Factorio Wiki with our own python code, which will be very useful in the future when we what to test several scenarios and do some data analysis. We will start our python implementation of these quality concepts by writing a function $f(q)$ that returns a 5x5 probability matrix $Q_q$:
class QualityTier(IntEnum):
Normal = 0
Uncommon = 1
Rare = 2
Epic = 3
Legendary = 4
def quality_probability(
quality_chance : float,
input_tier : QualityTier,
output_tier : QualityTier) -> float:
"""Calculates the probability of a machine craft with a certain `quality_chance` upgrading
the resulting product from the tier of the products (`input_tier`) to the `output_tier`.
Args:
quality_chance (float): Quality chance (in %).
input_tier (QualityTier): Quality tier of the ingredients.
output_tier (QualityTier): Quality tier of the product.
Returns:
float: A probability from 0 to 1.
"""
# Some QoL conversions
quality_chance /= 100
i = input_tier
o = output_tier
# An item can never be downgraded
if input_tier > output_tier:
return 0
# If the item is already legendary, it will remain legendary
if input_tier == QualityTier.Legendary:
return 1
# Probability of item staying in the same tier
if input_tier == output_tier:
return 1 - quality_chance
# Probability of item going straight to legendary
if output_tier == QualityTier.Legendary:
return quality_chance / (10 ** (3 - i))
# else
return (quality_chance * 9/10) / (10 ** (o - i - 1))
def quality_matrix(quality_chance : float) -> np.ndarray:
"""Returns the quality matrix for the corresponding `quality_chance` which indicates
the probabilities of any input tier jumping to any other tier.
Args:
quality_chance (float): Quality chance (in %).
Returns:
np.ndarray: 5x5 matrix. The columns represent the input quality tier and go
from legendary to normal, from left to right. The lines represent the output
quality tier and go from normal to legendary, from top to bottom.
"""
res = np.zeros((5,5))
for row in range(5):
for column in range(5):
res[row][column] = quality_probability(quality_chance, row, column)
return res
Calling quality_matrix(10) returns the following result:
$$Q_{10} = \begin{bmatrix} 0.9 & 0.09 & 0.009 & 0.0009 & 0.0001 \\ 0 & 0.9 & 0.09 & 0.009 & 0.001 \\ 0 & 0 & 0.9 & 0.09 & 0.01 \\ 0 & 0 & 0 & 0.9 & 0.1 \\ 0 & 0 & 0 & 0 & 1 \\ \end{bmatrix}$$
Which perfectly matches the table in the wiki:

(image source: Factorio Wiki)
Building the production matrix Link to heading
Production ratio Link to heading
Now that we have our quality matrix we can use it as a basis for creating production matrices that reflect any crafting or recycling scenario. For any crafting situation there are only two values we need to worry about: the quality chance of the machine and the production ratio of output items relative to input items.
We have already talked extensively about the quality chance, so let’s take a moment to understand how to come up with a production ratio for an arbitrary scenario. Let’s take blue circuits as an example:
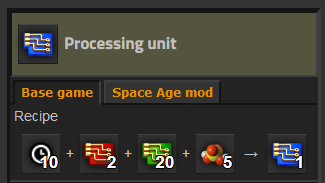
(image source: Factorio Wiki)
In order to craft a single blue circuit you need 22 solid ingredients, leading to a rather low production ratio of 0.04545. Luckily for us, we haven’t factored in productivity yet. Let’s assume that:
- We researched 3 levels of blue circuit productivity (+30% Productivity)
- The circuits are being crafted in a EM Plant (+50% Productivity)
- The EM plant has one tier 3 productivity module (+10% Productivity)
In total we have a 90% productivity bonus, which means we get a borderline 2 for 1 deal for blue circuit crafting. We can now update our production ratio value:
$$ r = \frac{o}{i} (1 + p) = \frac{1}{22} (1 + \frac{9}{10}) = \frac{19}{220} = 0.0863636$$
Production matrix Link to heading
Building a basic production matrix is as simple as multiplying the corresponding quality matrix by the production ratio:
$$ P_{q, r} = r Q_q $$
The corresponding python function is just as straightforward:
def basic_production_matrix(quality_chance : float, production_ratio : float) -> np.ndarray:
"Returns the production matrix for the corresponding quality_chance and production_ratio"
return quality_matrix(quality_chance) * production_ratio
Now that we know the basics, let’s calculate the production matrix for the EM plant from the previous subchapter, which has 1 T3 productivity module and 4 T3 quality modules (i.e. 10% quality chance):
$$ P_{10, \frac{19}{220}} = \frac{19}{220} Q_{10} = \begin{bmatrix} 0.07772727 & 0.00777273 & 0.00077727 & 0.00007773 & 0.00000864 \\ 0 & 0.07772727 & 0.00777273 & 0.00077727 & 0.00008636 \\ 0 & 0 & 0.07772727 & 0.00777273 & 0.00086364 \\ 0 & 0 & 0 & 0.07772727 & 0.00863636 \\ 0 & 0 & 0 & 0 & 0.08636364 \\ \end{bmatrix}$$
This matrix is completely fine at first glance, but what if we want to anything even remotely complex?
- If we’re crafting with legendary ingredients, why not load the EM Plant with the best productivity modules you have?
- What if we want to remove all legendary items from the system?
- What if want my EM Plants to have more quality modules for lower quality items, and more productivity modules for the higher quality items?
The solution for these issues is to have the ability to customize the quality chance & production ratio for every row in the matrix:
def custom_production_matrix(parameters_per_row : List[Tuple[float, float]]) -> np.ndarray:
"""Returns a production matrix where every row has a specific quality chance
and prodution ratio.
Args:
parameters_per_row (List[Tuple[float, float]]): List of five tuples. Each tuple
indicates the quality chance (%) and production ratio for the respective row.
Returns:
np.ndarray: 5x5 production matrix.
"""
res = np.zeros((5,5))
for row in range(5):
quality_chance, production_ratio = parameters_per_row[row]
for column in range(5):
res[row][column] =\
quality_probability(quality_chance, row, column) * production_ratio
return res
Now that we’re armed with this new function, we can easily modify the EM scenario in order to only have productivity modules when crafting with legendary items:
print(custom_production_matrix([(10, (1 + 0.9)/22)] * 4 + [(0, (1 + 1.3)/22)]))
# [[0.07772727 0.00777273 0.00077727 0.00007773 0.00000864]
# [0. 0.07772727 0.00777273 0.00077727 0.00008636]
# [0. 0. 0.07772727 0.00777273 0.00086364]
# [0. 0. 0. 0.07772727 0.00863636]
# [0. 0. 0. 0. 0.10454545]]
How to use the production matrix: a simple exercise Link to heading
We have spent all this time coming up with this production matrices, but we still don’t know how to use them. Let’s change that by solving a simple exercise:
A recycler with 2 rare and 2 epic T3 quality modules is being fed iron plates of several qualities:
- 10 normal iron plates/s
- 5 rare iron plates/s
- 4 epic iron plates/s
How many iron plates of each quality level are being produced by the recycler?
Our first step is to calculate the quality chance $q$:
$$ q = 4 * 2 + 4.7 * 2 = 17.6\% $$
The production ratio $r$ of a recycler is quite straightforward to calculate, but please note that the input $i$ and output $o$ of a recipe are switched in the production ratio formula because we are recycling:
$$ r = \frac{i}{o} (1 + p) = \frac{i}{o} (1 + (- 0.75)) = \frac{i}{4o}$$
Iron plates recycle into themselves, which means $i = o = 1$ and the production ratio $r$ is 0.25. We can now create the production matrix for the recycler:
custom_production_matrix([(17.6, 0.25)] * 5)
$$ \begin{bmatrix} 0.206 & 0.0396 & 0.00396 & 0.000396 & 0.000044 \\ 0 & 0.206 & 0.0396 & 0.00396 & 0.00044 \\ 0 & 0 & 0.206 & 0.0396 & 0.0044 \\ 0 & 0 & 0 & 0.206 & 0.044 \\ 0 & 0 & 0 & 0 & 0.25 \\ \end{bmatrix}$$
Notice how the numbers of each row add up to the production ratio value of 0.25, as we expected.
We have our recycler in the form of a matrix, we’re only missing the intake for it, which will be represented by a row vector with five values (one for each level of quality):
$$ \vec{f} = \begin{bmatrix} 10 & 0 & 5 & 4 & 0 \end{bmatrix}$$
In order to get the solution $\vec{s}$ for our little exercise, we simply multiply $\vec{f}$ by the production matrix of the recycler:
np.array([10, 0, 5, 4, 0]) @ custom_production_matrix([(17.6, 0.25)] * 5)
$$ \vec{s} = \begin{bmatrix} 10 & 0 & 5 & 4 & 0 \end{bmatrix} \cdot \begin{bmatrix} 0.206 & 0.0396 & 0.00396 & 0.000396 & 0.000044 \\ 0 & 0.206 & 0.0396 & 0.00396 & 0.00044 \\ 0 & 0 & 0.206 & 0.0396 & 0.0044 \\ 0 & 0 & 0 & 0.206 & 0.044 \\ 0 & 0 & 0 & 0 & 0.25 \\ \end{bmatrix} $$
$$ \vec{s} = \begin{bmatrix} 2.06 & 0.396 & 1.0696 & 1.02596 & 0.19844 \end{bmatrix}$$
We can confidently say that the recycler will produce:
- 2.06 normal iron plates/s
- 0.396 uncommon iron plates/s
- 1.0696 rare iron plates/s
- 1.02596 epic iron plates/s
- 0.19844 legendary iron plates/s
Next step: Pure Recycler Loop Link to heading
We have a mathematical foundation firmly set in place. Our attention will now turn towards solving specific quality grinding scenarios starting with the simplest of them all: a pure recycler loop.
-
I’m particularly fond of the effort and research that has gone into belt balancers. ↩︎
-
Or a recycler, crusher, smelter, etc. All of them are valid quality module recipients. ↩︎