The recycler-assembler loop is probably the most commonly used quality grinding method in Factorio. It is a two step looping process where in the first step, the ingredients are crafted by an assembler into items, which are then recycled back into ingredients. By having quality and productivity1 modules in both the assembling and the recycling steps, the quality and items and ingredients in the loop will eventually improve all the way to legendary quality. Emulating a recycler-assembler loop is slightly more complex than the pure recycling loops we have dealt with previously, but the same fundamental ideas still apply. Please note that functions from previous blog posts will be reused here.

(Credit for this design: Konage)
Unrolling the infinite loop Link to heading
Before we start crafting transition matrices, we need to figure out a way to deal with the outputs of the system getting fed back into the system2:
---
title: Conceptual model of a recycler-assembler loop
config:
theme: dark
---
flowchart TD
A[Ingredient Input] -->|Q=0 Ingredients| B[Assembler]
B -->|Q<=4 Items| C[Recycler]
C -->|Q<=4 Ingredients| B
B -->|Q=5 Items| D[Q5 Item Storage]
C -->|Q=5 Ingredients| E[Q5 Ingredient Storage]
Notice how I’m using “Q” as a shorthand for the level of quality of the items. Q=1 means common items and Q=5 means legendary items.
Finding a way to get around loops is never easy. Fortunately for us, we can take a page from a compiler optimization book and unroll the loop:
---
title: Conceptual model of a recycler-assembler loop, unrolled into an infinite line
config:
theme: dark
---
flowchart TD
A[Ingredient Input] --> A0
A0 -->|Q<=4 Items| R0
A0 -->|Q=5 Items| END[Q5 Item/Ingredient Storage]
R0 -->|Q=5 Ingredients| END
R0 -->|Q<=4 Ingredients| A1
A1 -->|Q=5 Items| END
A1 -->|Q<=4 Items| R1
R1 -->|Q=5 Ingredients| END
R1 -->|Q<=4 Ingredients|An[An]
An -->|Q=5 Items| END
An -->|Q<=4 Items|Rn1[Rn]
Rn1 -->|Q=5 Ingredients| END
Rn1 -->|Q<=4 Ingredients|Rn2[...]
Doing this trick does get rid of the loop and gives us a more workable linear problem. Unfortunately, this comes at a cost of having to handle the recycler-assembler line being theoretically infinite. In practice, the system runs out of materials very quickly because all the materials that don’t get voided will eventually turn into legendary items/ingredients and will get removed from the system.
Crafting a transition matrix Link to heading
An initial approach Link to heading
In theory, we could use the techniques we created in previous blog posts to calculate the outputs of this recycler-assembler line. We would need to know:
- The production matrix of the recycler $R$.
- The production matrix of the assembler $A$.
- An input vector of ingredients $\vec{a_0}$.
- Let’s assume that $\vec{a_0}= \begin{bmatrix} 1 & 0 & 0 & 0 & 0 \end{bmatrix}$ by default.
- What is the output of the system and what gets recycled (items/ingredients, and of which quality).
- This information would be incorporated in $A$ and $R$ by zeroing out the necessary matrix rows.
The state of the system would be represented by two vectors $\vec{a_x}$ and $\vec{r_x}$, which respectively represent the amount of ingredients and items after iteration $x$. In order to process $\vec{a_x}$ into $\vec{r_x}$ and vice versa, you must use the production matrices $R$ and $A$:
$$ \vec{a_x} = \vec{r_{x}} \cdot R $$
$$ \vec{r_x} = \vec{a_{x-1}} \cdot A $$
The final step would be to collect the production statistics after every iteration:
$$ \vec{a} = \vec{a_0} + \vec{a_1} + \vec{a_2} + \vec{a_3} + \vec{a_4} + \vec{a_n} + \vec{a_{n+1}} + …$$
$$ \vec{r} = \vec{r_1} + \vec{r_2} + \vec{r_3} + \vec{r_4} + \vec{r_n} + \vec{r_{n+1}} + …$$
I theory, this approach would work. In practice, however, having to flip-flop between items and ingredient vectors constantly is very annoying, confusing and hard to implement correctly without bugs. Luckily, we can make our lives a lot easier by having the matrix do the flip-flopping for us.
Introducing stochastic matrices Link to heading
A stochastic matrix is a a square matrix whose values represent the probability of a state transitioning to another state3. They are incredibly useful in a multitude of scientific fields and are also known as probability matrices, Markov matrices, substitution matrices, or, as the Factorio wiki prefers to call them, transition matrices.
In our case, we have two states: ingredient and item. We also have two transitions: item->ingredient and ingredient->item. Creating the transition matrix $M$ for this simple use case is quite straightforward:
$$ M = \begin{bmatrix} 0 & 1 \\ 1 & 0 \\ \end{bmatrix} $$
Let’s say that we have an input vector $\vec{v_0} = \begin{bmatrix} 1 & 0\end{bmatrix}$ whose first value represents the ingredients and the second value represents the items. Let’s multiply $\vec{v}$ by $M$:
$$ \vec{v_1} = \vec{v_0} \cdot M = \begin{bmatrix} 1 & 0\end{bmatrix} \cdot \begin{bmatrix} 0 & 1 \\ 1 & 0 \\ \end{bmatrix} = \begin{bmatrix} 0 & 1\end{bmatrix}$$
The values of the vector flipped! Let’s try it again:
$$ \vec{v_2} = \vec{v_1} \cdot M = \begin{bmatrix} 0 & 1\end{bmatrix} \cdot \begin{bmatrix} 0 & 1 \\ 1 & 0 \\ \end{bmatrix} = \begin{bmatrix} 1 & 0\end{bmatrix}$$
The values flipped back!! This is exactly the behaviour we need from a matrix. Now we only have to find a way to fit our recycler and assembler matrices in $M$.
Assembling the transition matrix Link to heading
We have everything we need to assemble our transition matrix $T$. Let’s assume that the assembler has a productivity of 50% and both the assembler and the recycler have a quality chance of 25%. Let’s also assume that we only want to keep the legendary items of the loop. $A$ and $R$ would look like this:
# The code and logic behind custom_production_matrix()
# was already explained in previous blog posts.
print(custom_production_matrix([(25, 1.5)] * 5)) # Assembler
print(custom_production_matrix([(25, 0.25)] * 4 + [(0, 0)])) # Recycler
$$ A = \begin{bmatrix} 1.125 & 0.3375 & 0.03375 & 0.003375 & 0.000375\\ 0 & 1.125 & 0.3375 & 0.03375 & 0.00375 \\ 0 & 0 & 1.125 & 0.3375 & 0.0375 \\ 0 & 0 & 0 & 1.125 & 0.375 \\ 0 & 0 & 0 & 0 & 1.5 \\ \end{bmatrix} $$
$$ R = \begin{bmatrix} 0.1875 & 0.05625 & 0.005625 & 0.0005625 & 0.0000625\\ 0 & 0.1875 & 0.05625 & 0.005625 & 0.000625 \\ 0 & 0 & 0.1875 & 0.05625 & 0.00625 \\ 0 & 0 & 0 & 0.1875 & 0.0625 \\ 0 & 0 & 0 & 0 & 0 \\ \end{bmatrix} $$
Notice how the last row of $R$ is zeroed out so that the legendary items are removed from our system. Let’s design our transition matrix $T$ (with some inspiration from the stochastic matrix we created in the previous subchapter):
$$T = \begin{bmatrix} 0 & A \\ R & 0 \\ \end{bmatrix} $$
The only thing left to do is to replace $A$ and $R$ with actual values:
def custom_transition_matrix(
recycler_matrix : np.ndarray,
assembler_matrix : np.ndarray) -> np.ndarray:
"""Creates a transition matrix based on the
provided recycler and assembler production matrices.
Args:
recycler_matrix (np.ndarray): Recycler production matrix.
assembler_matrix (np.ndarray): Assembler production matrix.
Returns:
np.ndarray: Transition matrix with the recycler production matrix
in the lower left and assembler production matrix in the upper right.
"""
res = np.zeros((10,10))
for i in range(5):
for j in range(5):
res[i + 5][j] = recycler_matrix[i, j]
res[i][j + 5] = assembler_matrix[i, j]
return res
if __name__ == "__main__":
print(custom_transition_matrix(
custom_production_matrix([(25, 0.25)] * 4 + [(0, 0)]),
custom_production_matrix([(25, 1.5)] * 5)
))
# [[0. 0. 0. 0. 0. 1.125 0.3375 0.03375 0.003375 0.000375]
# [0. 0. 0. 0. 0. 0. 1.125 0.3375 0.03375 0.00375 ]
# [0. 0. 0. 0. 0. 0. 0. 1.125 0.3375 0.0375 ]
# [0. 0. 0. 0. 0. 0. 0. 0. 1.125 0.375 ]
# [0. 0. 0. 0. 0. 0. 0. 0. 0. 1.5 ]
# [0.1875 0.05625 0.005625 0.0005625 0.0000625 0. 0. 0. 0. 0. ]
# [0. 0.1875 0.05625 0.005625 0.000625 0. 0. 0. 0. 0. ]
# [0. 0. 0.1875 0.05625 0.00625 0. 0. 0. 0. 0. ]
# [0. 0. 0. 0.1875 0.0625 0. 0. 0. 0. 0. ]
# [0. 0. 0. 0. 0. 0. 0. 0. 0. 0. ]]
$$ T = $$
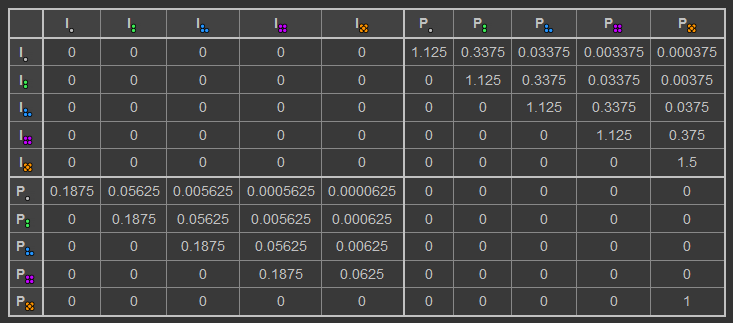
$$\small{\begin{bmatrix} 0 & 0 & 0 & 0 & 0 & 1.125 & 0.3375 & 0.03375 & 0.003375 & 0.000375 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1.125 & 0.3375 & 0.03375 & 0.00375 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1.125 & 0.3375 & 0.0375 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1.125 & 0.375 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1.5 \\ 0.1875 & 0.05625 & 0.005625 & 0.0005625 & 0.0000625 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0.1875 & 0.05625 & 0.005625 & 0.000625 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0.1875 & 0.05625 & 0.00625 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0.1875 & 0.0625 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ \end{bmatrix}} $$
$T$ matches4 the matrix in the Factorio wiki, which is a good sign that we generated this matrix correctly:
Calculating the production rate of the infinite recycler-assembler line Link to heading
In order to get the total production of Q5 items (or ingredients), we have to add the Q5 production of every single recycler and assembler in the infinite chain:
$$ \vec{t} = \vec{t_0} + \vec{t_1} + \vec{t_2} + \vec{t_3} + \vec{t_4} + \vec{t_n} + \vec{t_{n+1}} + …$$
$\vec{t_x}$ is the state of the system after one loop of recycler and assembler $x$. The first five values represent the ingredients in the system (from Q0 in the first position to Q5 in the fifth position) and the last five values represent the items in the system (with the quality increasing from left to right likewise). $\vec{t_x}$ can be calculated in the following manner:
$$ \vec{t_x} = \vec{t_{x-1}} \cdot T $$
$T$ is the previously discussed transition matrix. $ \vec{t_0} $ represents the input of the system, which by default is a belt of common items:
$$ \vec{t_0} = \begin{bmatrix} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \end{bmatrix} $$
We have everything needed to start simulating a recycler-assembler loop. Luckily for us, the code that was written to simulate pure recycler loops won’t require too many tweaks to work with transition matrices:
input_vector = np.array([1] + [0] * 9)
# Transition matrix from the previous chapter
transition_matrix = custom_transition_matrix(
custom_production_matrix([(25, 0.25)] * 4 + [(0, 0)]),
custom_production_matrix([(25, 1.5)] * 5)
)
result_flows = [input_vector]
while True:
result_flows.append(result_flows[-1] @ transition_matrix)
if sum(abs(result_flows[-2] - result_flows[-1])) < 1E-10:
# There's nothing left in the system
break
print(sum(result_flows))
# [1.26732673 0.20327419 0.08342292 0.02966277 0.00632351 1.42574257 0.65640623 0.2052281 0.07266358 0.02497469]
Simulating a recycler-assembler loop with the transition matrix from the previous chapter yields the following result:
$$\vec{t} = \begin{bmatrix} 1.267 & 0.203 & 0.083 & 0.0297 & 0.0063 & 1.426 & 0.656 & 0.205 & 0.073 & 0.02497 \end{bmatrix}$$
Feeding 1 belt of ingredients to this loop will result in 0.02497 belts of legendary items being produced. In other words, this setup has an efficiency of 2.497%.
These are the fundamentals of simulating recycler-assembler loops. Now, all that remains to be done is to determine which questions about this quality grinding method should be asked, and how to answer them with the tools we have at our disposal.
The recycler_assembler_loop() function Link to heading
The simulation code from the previous chapter works well enough for simple cases. Nevertheless, if we wish to simulate tons of variations in setups, we’ll need a solution that doesn’t involve having to manually calculate the productivity and quality chance of every row of the transition matrix.
Having felt the need for a higher level approach to simulating recycler-assembler loops (so that I could stop dealing with productivity bonuses and quality chances and start dealing with quality and productivity modules), I came up with the following function:
def recycler_assembler_loop(
input_vector : Union[np.array, float],
assembler_modules_config : Union[Tuple[float, float], List[Tuple[float, float]]],
items_quality_to_keep : Union[int, None] = 5,
ingredients_quality_to_keep : Union[int, None] = 5,
base_prod_bonus : float = 0,
recipe_ratio : float = 1,
prod_module_bonus : float = 25,
qual_module_bonus : float = 6.2) -> np.array:
# The docstring was cut from this code snippet for the sake of brevity
if type(assembler_modules_config) == tuple:
assembler_modules_config = [assembler_modules_config] * 5
# Parameters for the production matrices
recycler_parameters = get_recycler_parameters(
items_quality_to_keep if items_quality_to_keep != None else 6,
recipe_ratio,
qual_module_bonus
)
assembler_parameters = get_assembler_parameters(
assembler_modules_config,
ingredients_quality_to_keep if ingredients_quality_to_keep != None else 6,
base_prod_bonus,
recipe_ratio,
prod_module_bonus,
qual_module_bonus
)
if type(input_vector) in (float, int):
input_vector = np.array([input_vector] + [0] * 9)
result_flows = [input_vector]
while True:
result_flows.append(
result_flows[-1] @ custom_transition_matrix(
custom_production_matrix(recycler_parameters),
custom_production_matrix(assembler_parameters)
)
)
if sum(abs(result_flows[-2] - result_flows[-1])) < 1E-10:
# There's nothing left in the system
break
return sum(result_flows)
For the sake of keeping the the code snippet above as short as possible, I decided to leave out the auxiliary functions get_recycler_parameters and get_assembler_parameters, and the docstring for the function above5. Given that we don’t have a doc string, I will instead explain below what this function does in writing.
recycler_assembler_loop() details Link to heading
The recycler_assembler_loop() function simulates a recycler-assembler loop by unrolling the loop into a line and processing the ingredients and items in the system until there is nothing left. The successive states of the system are then all added up and returned as a vector with 10 values. The first five values represent the ingredients and the last five values represent the items, going from common to legendary.
The values of the vector mean different things, depending on whether items/ingredients of that quality are kept or reprocessed by the system:
- If they are kept: the value is the production rate of ingredients/items of that quality level.
- If they are reprocessed: the value is the internal flow rate of ingredients/items of that quality level in the system.
This function has eight arguments:
input_vector: The input vector of the system.assembler_modules_config: The module configuration (i.e. number of productivity and quality modules) of the assemblers of the system. Some examples:- Let’s say that you want to load every assembler with quality modules:
(0, 4). - Now let’s say that we want to load the legendary item crafter with productivity modules instead:
[(0, 4), (0, 4), (0, 4), (0, 4), (4, 0)].
- Let’s say that you want to load every assembler with quality modules:
items_quality_to_keep: Minimum quality level of the items to be removed from the system. If set toNone, nothing is removed and all items are reprocessed.ingredients_quality_to_keep: Minimum quality level of the ingredients to be removed from the system. If set toNone, nothing is removed and all ingredients are reprocessed.base_prod_bonus: Base productivity of assembler + productivity technologies (as a %).recipe_ratioRatio of items to ingredients of the crafting recipe.prod_module_bonus: Productivity bonus from productivity modules. Defaults to 25%.qual_module_bonus: Quality chance bonus from quality modules. Defaults to 6.2%.
With this function, we will be able to easily calculate the efficiency of every possible module allocation in the assemblers of the loop.
Statistical analysis Link to heading
In this final chapter, we will focus on calculating the efficiency of every relevant module configuration for every type of assembler. We will have to control for four variables:
- Number of modules (assembler-specific).
- Base productivity without modules (assembler-specific).
- What is the output of the system (
IngredientsorItems)6. - How should the modules be placed in the assemblers (
FullQuality,FullProductivity,Optimize).
The input to the system will consist of a belt of normal ingredients.
The function below takes the four previously mentioned variables as arguments and outputs an efficiency value as a percentage:
def recycler_assembler_efficiency(
module_slots : int,
base_productivity : float,
system_output : SystemOutput,
module_strategy : ModuleStrategy) -> float:
"Returns the efficiency of the setup with the given parameters (%)."
assert module_slots >= 0 and base_productivity >= 0
if system_output == SystemOutput.ITEMS:
keep_items = 5
keep_ingredients = None
else: # system_output == SystemOutput.INGREDIENTS:
keep_items = None
keep_ingredients = 5
# What is the output of the system: ingredients or items?
result_index = 4 if system_output == SystemOutput.INGREDIENTS else 9
if module_strategy != ModuleStrategy.OPTIMIZE:
if module_strategy == ModuleStrategy.FULL_PRODUCTIVITY:
config = (module_slots, 0)
else:
config = (0, module_slots)
output = recycler_assembler_loop(
100, config, keep_items, keep_ingredients, base_productivity)
return output[result_index]
else:
best_config = None
best_efficiency = 0
all_configs = get_all_configs(module_slots)
for config in tqdm(list(all_configs)):
if config[4] != (module_slots, 0):
# Makes no sense to put quality modules on legendary item crafter
continue
output = recycler_assembler_loop(
100, list(config), keep_items, keep_ingredients, base_productivity)
efficiency = float(output[result_index])
if best_efficiency < efficiency:
best_config = config
best_efficiency = efficiency
return best_efficiency
Let’s say that we want to calculate the efficiency of a recycler-assembler loop with cryogenic plants where you only take the items and the module configuration is optimized:
print(f"{recycler_assembler_efficiency(8, 0, SystemOutput.ITEMS, ModuleStrategy.OPTIMIZE)}%")
# 14.505597006563411%
Alternatively, you might want to use EM plants instead:
print(f"{recycler_assembler_efficiency(5, 50, SystemOutput.ITEMS, ModuleStrategy.OPTIMIZE)}%")
# 7.556345820541531%
And what if you’re crafting blue circuits and have 10 levels of blue circuit productivity?
productivity_research = 10
efficiency = recycler_assembler_efficiency(
5, 50 + productivity_research * 10, SystemOutput.ITEMS, ModuleStrategy.OPTIMIZE)
print(f"{efficiency}%")
# 156.67377286511638%
Woah, 156.67%?! We’re pretty much getting 3 legendary items for every two common ingredients. The reason for this anomaly is the absurdly high level of productivity of the EM plants (275%) and the fact that our input belt of ingredients transforms into 3.75 belts of items before being touched by a single recycler. In matter of fact, if we get to level 13 of blue circuit productivity we should hit an “efficiency” of 400%, which reflects a limit imposed by the game to prevent net-positive recycling loops:
productivity_research = 13
efficiency = recycler_assembler_efficiency(
5, 50 + productivity_research * 10, SystemOutput.ITEMS, ModuleStrategy.OPTIMIZE)
print(f"{efficiency}%")
# 399.9999999999473%
If we change the system output to ingredients, the efficiency number should make a lot more sense:
productivity_research = 13
efficiency = recycler_assembler_efficiency(
5, 50 + productivity_research * 10, SystemOutput.INGREDIENTS, ModuleStrategy.OPTIMIZE)
print(f"{efficiency}%")
# 99.99999999998285%
As expected, the system is lossless.
Efficiency table for all assembler types Link to heading
The only thing we haven’t done yet7 is a table with every possible assembler type and every possible system output and module strategy combination:
DATA = { # (number of slots, base productivity)
"Electric furnace/Centrifuge" : (2, 0),
"Chemical Plant" : (3, 0),
"Assembling machine" : (4, 0),
"Foundry/Biochamber" : (4, 50),
"Electromagnetic plant" : (5, 50),
"Cryogenic plant" : (8, 0),
}
OUTPUTS = (SystemOutput.ITEMS, SystemOutput.INGREDIENTS)
STRATEGIES = (
ModuleStrategy.FULL_QUALITY,
ModuleStrategy.FULL_PRODUCTIVITY,
ModuleStrategy.OPTIMIZE
)
KEY_NAMES = {
(SystemOutput.ITEMS, ModuleStrategy.FULL_QUALITY) : "(D) Quality only, max items",
(SystemOutput.ITEMS, ModuleStrategy.FULL_PRODUCTIVITY) : "(E) Prod only, max items",
(SystemOutput.ITEMS, ModuleStrategy.OPTIMIZE) : "(F) Optimal modules, max items",
(SystemOutput.INGREDIENTS, ModuleStrategy.FULL_QUALITY) : "(G) Quality only, max ingredients",
(SystemOutput.INGREDIENTS, ModuleStrategy.FULL_PRODUCTIVITY) : "(H) Prod only, max ingredients",
(SystemOutput.INGREDIENTS, ModuleStrategy.OPTIMIZE) : "(I) Optimal modules, max ingredients",
}
table = {key : {} for key in DATA}
for assembler_type, (slots, base_prod) in DATA.items():
for output in OUTPUTS:
for strategy in STRATEGIES:
eff = recycler_assembler_efficiency(slots, base_prod, output, strategy)
table[assembler_type][KEY_NAMES[(output, strategy)]] = eff
print(pandas.DataFrame(table).T.to_string())
# (D) Quality only, (E) Prod only, (F) Optimal modules, (G) Quality only, (H) Prod only, (I) Optimal modules,
# max items max items max items max ingredients max ingredients max ingredients
# Electric furnace/Centrifuge 0.264155 0.197364 0.324414 0.156426 0.131576 0.174408
# Chemical Plant 0.435917 0.418846 0.656637 0.234063 0.239340 0.312047
# Assembling machine 0.646313 0.861710 1.251900 0.323126 0.430855 0.539714
# Foundry/Biochamber 2.452490 3.503164 4.124319 1.001224 1.401265 1.547671
# Electromagnetic plant 3.322265 7.074719 7.556346 1.299017 2.572625 2.657463
# Cryogenic plant 1.866389 14.505597 14.505597 0.786774 4.835199 4.835199
The values of this table perfectly match the work done by Konage:

This will conclude our statistical analysis of recycler-assembler loops. We only scratched the tip of the iceberg7 here, but this blog post is already way too long.
Next step? Up to you to decide Link to heading
This marks the end our journey unveiling the mathematical underpinnings of Factorio’s Quality feature. Please do note that there’s plenty left still to uncover and analyse (refer to this tooltip7), but if you reached this far you have every tool on your belt to chart a path by yourself.8 I’m no longer needed.
Lastly, I would like to thank you, the reader, for reading this blog post/series of blog posts. I hope you learned something interesting along the way.
-
Productivity modules are only allowed under certain circumstances in the assembling step, whereas quality modules are always allowed in both the recycling and assembling steps. ↩︎
-
You might be getting a strong feeling of déjà vu if you have already read “Solving the mathematics of Factorio Quality: Pure Recycler Loop” previously. ↩︎
-
There is an argument to be made that the quality and production matrices used throughout this series of blog posts are stochastic matrices. ↩︎
-
The
1in the bottom right corner of the wiki table doesn’t match with $T$. This is expected because I calculate the production rates in a slightly different way than most people do. ↩︎ -
All the code written for this series of blog posts can be found here. ↩︎
-
Outputting both legendary items and ingredients is also a valid possiblility, but we won’t consider that today. ↩︎
-
I’m paraphrasing here. There’s a ton of topics we haven’t touched in this series of blog posts, such as having inputs with some quality items/ingredients already, internal flow analysis of recycler-assembler loops (i.e. why it still makes sense to use legendary quality modules in lossless loops), efficiency of recycler-assembler loops when you feed it items instead of ingredients to name a few. ↩︎ ↩︎ ↩︎
-
If you are looking for a more practical approach to quality, I heartily recommend Konage’s comprehensive quality guide. ↩︎